Triangulu isusceli
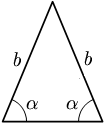
Hè difinitu com'è triangulu isusceli un triangulu chì pussedi almenu dui lati uguali è chì pussedi almenu dui anguli uguali. Infatti vali u siguenti tiurema: un triangulu hà dui lati uguali solu s'è hà dui anguli uguali è viciversa.
Stu tiurema custituisci a quinta prupusizioni di u Libru I di l'Elementi di Euclide è hè cunnisciutu com'è Pons asinorum, u "ponti di l'asini".
Particulari trianguli isusceli sò i trianguli equilateri è i trianguli rittanguli isusceli. Esistini ancu trianguli isusceli acutanguli è ottusanguli.
I trianguli isusceli rittanguli sò tutti simili trà eddi, com'è i trianguli equilateri.
Simitrii
mudificàUn triangulu isusceli chì ùn hè micca equilateru hè invarianti solu par a riflissioni rispettu à a bisettrici di l'angulu diffarenti da i dui rimanenti. U so gruppu di simitria, in più di à a trasfurmazioni idantità, cumprendi solu quista riflissioni è dunqua hè isumorfu à u gruppu di dui elementi, vali à dì à u gruppu multiplicativu nantu à l'insemu {1, −1}.
Trianguli isusceli in giumitria analitica
mudificàTiurema 1: Cundizioni nicissaria è sufficienti affinch'è un triangulu incù a basa parallela à l'assi sii isusceli hè ch'eddu agvissi i dui lati di cuefficienti angulari oppostu.
Dimustrazioni.
Dati i trè retti
si ni calculeghja l'intersizzioni.
Tandu si calculeghja a distanza di i sigmenti AC è BC.
Dunqua u triangulu hè isusceli nantu à a basa AB. Di manera analuga si dimostra u casu di a basa parallela à l'assi y.
Viciversa si custruisci un triangulu isusceli incù a basa parallela à l'assi di l'ascissi.
Dati i dui punti:
apposta ch'è u vertici d'un triangulu isusceli ghjaci nantu à a stessa retta di u puntu mediu di a basa, prima si trova è dopu .
Dunqua si trova , chì avarà listessa ascissa ch'è è diffarenti urdinata.
Si verificheghja ch'è u triangulu hè isusceli:
Tandu si calculeghja u cuefficienti angulari di i dui lati:
Tiurema 2: Cundizioni nicissaria è sufficienti affinch'è un triangulu incù a basa parallela à a bisettrici di dui quadranti sii isusceli hè ch'eddu avissi i dui lati di cuefficienti angulari inversi.
Dimustrazioni.
Dati i trè retti
si ni calculeghja l'intersizzioni.
Tandu si calculeghja a distanza di i sigmenti AC è BC.
Dunqua u triangulu hè isusceli nantu à a basa AB. In modu analugu si dimostra u casu di a basa parallela à l'assi y.
Viciversa si custruisci un triangulu isusceli incù a basa parallela à a bisettrici di u prima è terzu quadranti. (Listessa cosa vali par quidda parallela à a bisettrici di u sicondu è quartu quadranti).
Dati i dui punti:
postu ch'è u vertici d'un triangulu isusceli ghjaci nantu à a stessa retta di u puntu mediu di a basa, prima si trova è eppo/dopu .
Dunqua si trova , chì si trova nantu à a retta parpindiculari à a basa è passanti par , .
induva h hè un numaru arbitrariu diffarenti da 0.
Si verificheghja chì u triangulu hè isusceli:
Tandu si calculeghja u cuefficienti angulari di i dui lati:
Da veda dinò
mudificà- Triangulu
- Triangulu equilateru
- Triangulu scalenu
- Tiurema direttu di i trianguli isusceli
- Toru (giumitria)
- Giumitria piana
- Angulu rettu
- Catetu
- Mezaretta
- Perimetru
- Sigmentu
- Triangulu equilateru
- Tiurema di Pitagora
- Iputenusa
- Tangenti
- Trigunumitria
- Uttaedru
Noti
mudificà
Fonti
mudificà'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.