Triangulu rittangulu
U triangulu rittangulu (o triangulu rettangulu) hè un triangulu in u quali l'angulu furmatu da dui lati, ditti cateti, hè rettu, vali à dì di 90° (o π/2 radianti). U latu oppostu à l'angulu rettu si chjama iputenusa. L'iputenusa hè par via di u tiurema di Pitagora para à a radica quatrata di a somma di i quatrati di i cateti.
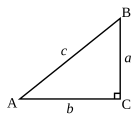
U triangulu rittangulu ripprisenta un casu particulari di triangulu genericu, par u quali molti rilazioni fundamintali si simplificheghjani. U casu più particulari hè quiddu di u triangulu rittangulu isusceli, casu par u quali
- .
Aghjunghjendu à un triangulu rittangulu u triangulu ottinutu incù a so riflissioni rispettu à l'iputenusa s'otteni un aquilonu. Aghjunghjendu li u triangulu ottinutu fendu una rutazioni di 'π intornu à u puntu mediu di l'iputenusa s'otteni u rittangulu par u quali l'iputenusa hè diagunali principali.
Da u triangulu rittangulu isusceli incùi dui custruzzioni s'otteni u quatratu di latu a = b.
Prubità
mudificàTiuremi Fundamintali (Prubità di i lati)
mudificà| Tiurema di Pitagora | |
| 1° Tiurema di Euclide | |
| 2° Tiurema di Euclide |
Prubità di l'anguli interni
mudificà- Sapendu ch'è a somma di l'anguli interni d'un triangulu qualunquai hè 180° (π rad), in u casu particulari d'un triangulu rittangulu, sapendu ch'è unu di l'anguli interni hè rettu tandu hè faciuli à diducia ch'è a somma di l'altri dui anguli interni vali sempri 90°:
- Da sta prubità si pò, par via di cunsiquenza, diducia ch'è s'edda hè tracciata l'altezza di u triangulu rittangulu incù a so urighjina in l'angulu rettu, dividi tandu 'ss'angulu in dui anguli minori, chjamati par asempiu θ è ω. Inoltri si sò à furmà dui trianguli rittanguli distinti (ACH è BCH) incù un catetu in cumunu, l'altezza par appuntu.
Par a prubità discritta sopra si pò dì ch'è:
- Cunsidarendu u Triangulu Rittangulu BCH, par a prubità vista sopra:
- Tandu si pò cunsidarà u Triangulu ABC cumplettu:
-
- da induva si diduci a prubità:
- Analugamenti si pò ussirvà ch'è:
-
Classi di similitudina
mudificàOgni trasfurmazioni di similitudina trasforma un triangulu rittangulu in un triangulu rittangulu è cusì hè utuli di cunsidarà i classi di similitudina di i trianguli rittanguli. Quiddi si poni ripprisintà currettamenti incù i trianguli rittanguli avendu l'iputenusa c di lunghezza 1 è u vertici oppostu appartinenti à una di i mezi circumfarenzi avendu com'è diamitru l'iputenusa. A cullizzioni di i classi di similitudina si pò parametrizà incù u rapportu à/b di i lunghezzi di i cateti vali à dì incù unu di i dui anguli micca retti, par asempiu incù l'angulu rilativu à u vertici A. A trigunumitria dici ch'è:
Trianguli Rittanguli Particulari
mudificàTriangulu Rittangulu isusceli
mudificàChjamatu ancu Triangulu 90-45 dati l'ampiezzi di l'anguli chì u formani, infatti hè cumpostu da un angulu rettu è dui anguli da 45°.
A carattaristica principali di stu triangulu hè ch'eddu hà i dui cateti uguali è misurani
Un'altra prubità di u triangulu rittangulu isusceli hè ch'è a midiana, l'altezza è a bisettrici rilativi à u vertici chì prisenta l'angulu rettu cuincidini. Inoltri toccani l'iputenusa asattamenti in u so puntu mediu, dividendu cusì tali latu in dui parti uguali incù lunghezza analoga à l'altezza/bisettrici/midiana tracciata.
Punti nutevuli
mudificàL'ortucentru d'un triangulu rittangulu cuincidi incù u vertici di l'angulu rettu.
U circucentru hè u puntu mediu di l'iputenusa.
Da veda dinò
mudificà
Noti
mudificà
Fonti
mudificà'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.
